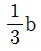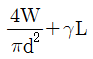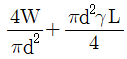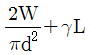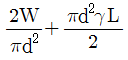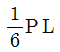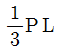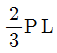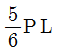1과목: 과목 구분 없음
1. 재료의 거동에 대한 설명으로 옳지 않은 것은?
- 탄성거동은 응력-변형률 관계가 보통 직선으로 나타나지만 직선이 아닌 경우도 있다.
- 크리프(creep)는 응력이 작용하고 이후 그 크기가 일정하게 유지되더라도 변형이 시간 경과에 따라 증가하는 현상이다.
- 재료가 항복한 후 작용하중을 모두 제거한 후에도 남는 변형을 영구변형이라 한다.
- 포아송비는 축하중이 작용하는 부재의 횡방향 변형률(ϵh)에 대한 축방향 변형률(ϵv)의 비(ϵv/ϵh)이다.
2. 그림과 같이 임의의 형상을 갖고 단면적이 A인 단면이 있다. 도심축(x0-x0)으로부터 d만큼 떨어진 축(x1-x1)에 대한 단면 2차모멘트가 Ix1일 때, 2d만큼 떨어진 축(x2-x2)에 대한 단면 2차모멘트 값은?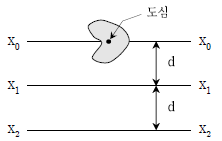
- Ix1+Ad2
- Ix1+2Ad2
- Ix1+3Ad2
- Ix1+4Ad2
3. 그림과 같이 보 구조물에 집중하중과 삼각형 분포하중이 작용할 때, 지점 A와 B에 발생하는 수직방향 반력 RA[kN]와 RB[kN]의 값은? (단, 구조물의 자중은 무시한다) (순서대로 RA, RB)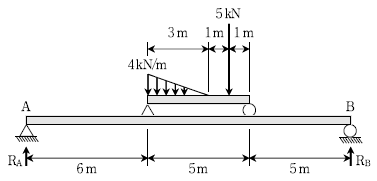
- 19/4, 25/4
- 23/4, 21/4
- 21/4, 23/4
- 25/4, 19/4
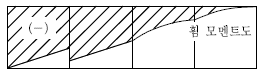
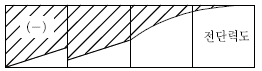
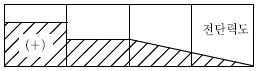
4. 그림과 같이 모멘트 M, 분포하중 w, 집중하중 P가 작용하는 캔틸레버 보에 대해 작성한 전단력도 또는 휨 모멘트도의 대략적인 형태로 적절한 것은? (단, 구조물의 자중은 무시한다)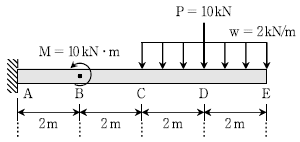
5. 그림과 같이 양단에서 각각 x만큼 떨어져 있는 B점과 C점에 내부힌지를 갖는 보에 분포하중 w가 작용하고 있다. A점 고정단 모멘트의 크기와 중앙부 E점 모멘트의 크기가 같아지기 위한 x값은? (단, 구조물의 자중은 무시한다)
- L/6
- L/5
- L/4
- L/3
6. 그림과 같이 수평으로 놓여 있는 보의 B점은 롤러로 지지되어 있고 이 롤러의 아래에 강체 블록이 놓여 있을 때, 블록이 움직이지 않도록 하기 위해 허용할 수 있는 힘 P[kN]의 최댓값은? (단, 블록, 보, 롤러의 자중은 무시하고 롤러와 블록 사이의 마찰은 없으며, 블록과 바닥 접촉면의 정지마찰계수는 0.3으로 가정한다)
- 1.2
- 1.8
- 2.4
- 3.0
7. 그림과 같은 하중이 작용하는 게르버 보에 대해 작성된 전단력도의 빗금 친 부분의 면적[kNㆍm]은? (단, 구조물의 자중은 무시한다)
- 9
- 51
- 60
- 69
8. 그림과 같이 절점 D에 내부힌지를 갖는 게르버 보의 A점에는 수평하중 P가 작용하고 F점에는 무게 W가 매달려 있을 때, 지점 C에서 수직 반력이 발생하지 않도록 하기 위한 하중 P와 무게 W의 비(P/W)는? (단, 구조물의 자중은 무시한다)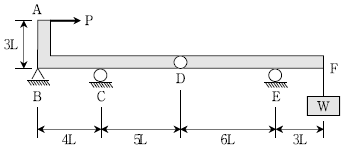
- 3/2
- 5/2
- 2/3
- 2/5
9. 그림과 같이 축하중 P를 받고 있는 기둥 ABC의 중앙 B점에서는 x방향의 변위가 구속되어 있고 양끝단 A점과 C점에서는 x방향과 z방향의 변위가 구속되어 있을 때, 기둥 ABC의 탄성좌굴을 발생시키는 P의 최솟값은? (단, 탄성계수  , 단면 2차모멘트 Ix=20π, Iz=π로 가정한다.)
, 단면 2차모멘트 Ix=20π, Iz=π로 가정한다.)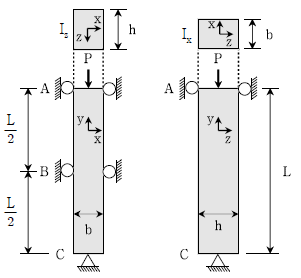
- 2π
- 4π
- 5π
- 20π
10. 그림과 같이 집중하중 P를 받는 캔틸레버 보에서 보의 높이 h가 폭 b와 같을 경우(h=b) B점의 수직방향 처짐량이 8mm라면, 동일한 하중조건에서 B점의 수직방향 처짐량이 27 mm가 되기 위한 보의 높이 h는? (단, 구조물의 자중은 무시하고 단면폭 b는 일정하게 유지한다)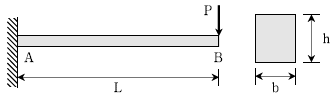
11. 그림과 같은 트러스에서 부재 BC의 부재력의 크기는? (단, 모든 부재의 자중은 무시하고, 모든 내부 절점은 힌지로 이루어져 있다)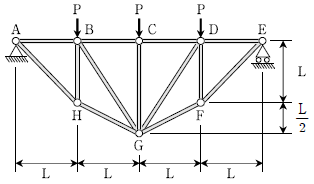
- P/3
- P
- 2P
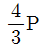
12. 그림과 같이 천장에 수직으로 고정되어 있는 길이 L, 지름 d인 원형 강철봉에 무게가 W인 물체가 달려있을 때, 강철봉에 작용하는 최대응력은? (단, 원형 강철봉의 단위중량은 γ이다)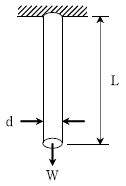
13. 그림과 같은 분포하중을 받는 보에서 B점의 수직반력(RB)의 크기는? (단, 구조물의 자중은 무시한다)
14. 그림과 같이 한 쪽 끝은 벽에 고정되어 있고 다른 한 쪽 끝은 벽과 1 mm 떨어져 있는 수평부재가 있다. 부재의 온도가 20°C 상승할 때, 부재 내에 발생하는 압축응력의 크기[kPa]는? (단, 보 부재의 탄성계수 E=2GPa, 열팽창계수 α=1.0 × 10-5/ °C이며, 자중은 무시한다)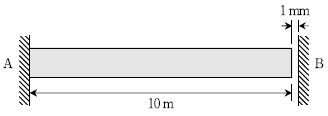
- 100
- 200
- 300
- 400
15. 그림과 같이 단위중량 γ, 길이 L인 캔틸레버 보에 자중에 의한 분포하중 w가 작용할 때, 보의 고정단 A점에 발생하는 휨 응력에 대한 설명으로 옳지 않은 것은? (단, 보의 단면은 사각형이고 전구간에서 동일하다)
- 폭 b가 2배가 되면 휨 응력값은 2배가 된다.
- 높이 h가 2배가 되면 휨 응력값은 1/2배가 된다.
- 단위중량 γ가 2배가 되면 휨 응력값은 2배가 된다.
- 길이 L이 2배가 되면 휨 응력값은 4배가 된다.
16. 그림과 같이 길이가 각각 1.505m, 1.500m이고 동일한 단면적을 갖는 부재 ⓐ와 ⓑ를 폭이 3.000 m인 강체 벽체 A와 C 사이에 강제로 끼워 넣었다. 이 때 부재 ⓐ는 δ1, 부재 ⓑ는 δ2만큼 길이가 줄어들었다면, 줄어든 길이의 비(δ1:δ2)는? (단, 부재의 자중은 무시하고, ⓑ의 탄성계수 E2가 부재 ⓐ의 탄성계수 E1의 3배이다)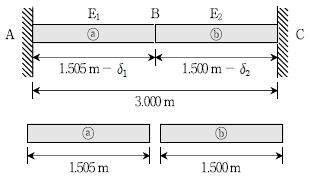
- 0.723 : 1.000
- 1.505 : 1.000
- 3.010 : 1.000
- 4.515 : 1.000
17. 그림과 같은 부정정보에서 B점의 고정단 모멘트[kNㆍm]의 크기는? (단, 구조물의 자중은 무시한다)
- 20
- 25
- 30
- 35
18. 그림과 같이 두 벽면 사이에 놓여있는 강체 구(질량 m=1 kg)의 중심(O)에 수평방향 외력(P=20 N)이 작용할 때, 반력 RA의 크기[N]는? (단, 벽과 강체 구 사이의 마찰은 없으며, 중력가속도는 10 m/s2로 가정한다)
- 15
- 20
- 25
- 30
19. 그림과 같이 재료와 길이가 동일하고 단면적이 각각 A1=1,000mm2, A2=500mm2인 부재가 있다. 부재의 양쪽 끝은 고정되어 있고 온도가 최초 대비 10 °C 올라갔을 때, 이로 인해 유발되는 A점에서의 반력 변화량[kN]은? (단, 부재의 자중은 무시하고 탄성계수 E=210 GPa, 열팽창계수 α=1.0 × 10-5/ °C이다)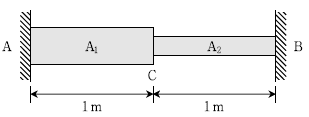
- 8.0
- 14.0
- 24.0
- 42.0
20. 그림과 같은 평면응력상태에 있는 미소요소에서 발생할 수 있는 최대 전단응력의 크기[MPa]는? (단, σx=36MPa, τxy=24MPa)
- 30
- 40
- 50
- 60