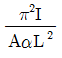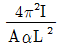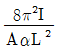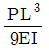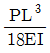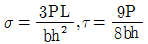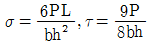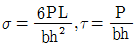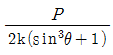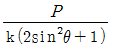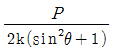1. 다음 중 옳지 않은 것은?
- 물체가 균질(Homogeneous)한 경우, 물체의 도심과 질량중심은 서로 일치한다.
- 단면의 형태에 따라 단면의 극관성모멘트는 음의 값을 가질 수도 있다.
- 평형방정식은 구조물의 재료의 성질에 관계없이 적용할 수 있다.
- 임의의 물체에 작용하는 우력모멘트는 일을 행한다.
2. 그림과 같이 2 kN과 4 kN의 하중이 4m 간격을 유지하며 이동 하고 있다. 지점 A와 B의 반력이 같게 될 때, 2 kN이 작용하는 위치로부터 A 지점까지의 거리 x [m]는?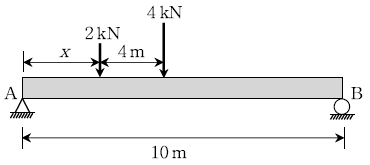
- 2.0
- 2.3
- 3.0
- 3.3
4. 그림과 같이 A점, C점이 스프링으로 연결된 보구조물이 등분포 하중을 받고 있을 때, 보중앙의 B점에 발생하는 연직 처짐[m]은? (단, 휨강성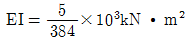 
이며, 스프링상수 k＝100 kN/m 이다.)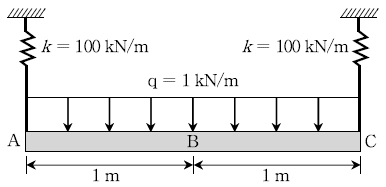
- 0.010
- 0.018
- 0.022
- 0.026
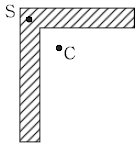
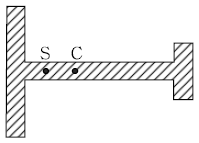
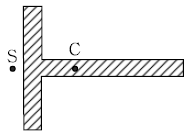
5. 구조부재 단면의 도심(C)과 전단중심(S)을 표시한 것으로 옳지 않은 것은?
6. 그림과 같이 높이가 2m인 댐이 두께 100 mm인 수직 목재보로 가설되었다. 직사각형 단면 목재보의 하단은 완전 고정되었고 물의 단위중량을 10 kN/m3으로 가정할 때, 목재보에 작용하는 최대 휨응력[MPa]은?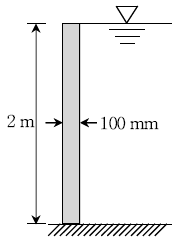
- 6
- 8
- 10
- 12
7. 그림과 같은 이상형 강체 기둥 모델의 좌굴임계하중은? (단, A 점은 힌지절점이고, B점은 선형탄성 거동을 하는 스프링에 연결되어 있으며, C점의 변위는 작다고 가정한다. BD구간의 스프링 상수는 k이다)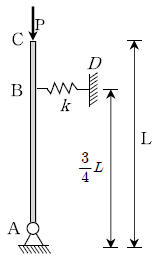
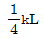
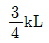
- 1kL
8. 그림과 같이 모래 위에 놓인 보 AB에서 점 D에 148 kN, 점 E에 200 kN의 집중하중과 AB의 중앙 C점에 모멘트하중 176 kNㆍm이 작용한다. 모래 지반에서의 반력은 A로 부터 B까지 직선적으로 분포한다고 가정할 때 148 kN이 작용되는 D점에서의 휨모멘트에 가장 가까운 값[kNㆍm]은?
- 28.0
- 29.6
- 31.5
- 33.2
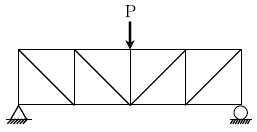
9. 다음 트러스 구조물 중에서 사재가 압축만 받는 구조물은?
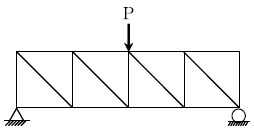
10. 그림과 같은 양단 고정 기둥에서 온도를 △T만큼 상승시켜 오일러좌굴을 발생시킬 때, 온도 상승량 △T의 값은? (단, 열팽창계수는 α이고, 휨강성은 EI이며, 단면적은 A이다)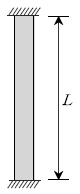
-
CBT문제은행AI2023-04-11 21:19
고정 기둥에서 발생하는 오일러좌굴은 다음과 같은 식으로 나타낼 수 있다.
여기서 P는 압력, L은 기둥의 길이, E는 탄성계수, I는 단면 2차 모멘트, A는 단면적, α는 열팽창계수이다.
따라서, 온도 상승량 △T는 다음과 같이 구할 수 있다.
따라서, 정답은 "
"이다.
11. 그림과 같은 구조물을 바르게 판별한 것은?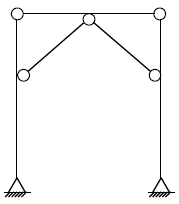
- 안정, 정정 구조물
- 안정, 1차부정정 구조물
- 불안정, 1차부정정 구조물
- 불안정, 2차부정정 구조물
12. 그림과 같이 양단고정보로 설계된 구조물에 대해 고정단 B에서 볼트체결이 충분하지 않다고 판단되어, B지점을 힌지로 바꾸어 안전성을 검토하려 한다. 이때 양단고정보와 비교하여 A지점의 모멘트와 보의 최대 모멘트의 절대치 크기에 대한 기술로 옳은 것은?
- A지점 모멘트 증가, 최대 모멘트 감소
- A지점 모멘트 증가, 최대 모멘트 증가
- A지점 모멘트 감소, 최대 모멘트 증가
- A지점 모멘트 감소, 최대 모멘트 감소
13. 그림과 같이 ac 구간은 단면적이 2A, cd 구간은 단면적이 A인 같은 재료의 봉이 있다. 하중 조건이 그림과 같을 때 점 d의 수평변위는? (단, E는 탄성계수이다)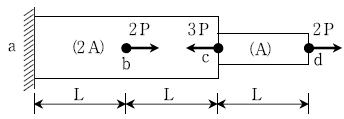
- 0
- PL/EA
- 2PL/EA
- 3PL/EA
14. 탄성체가 가지고 있는 탄성변형에너지를 작용하고 있는 하중으로 편미분하면 그 하중점에서 작용하는 변위가 된다는 정리는?
- Maxwell 상반정리
- Mohr의 모멘트－면적정리
- Betti의 정리
- Castigliano의 제2정리
15. 그림과 같이 동일한 재료를 사용하여 양단이 고정된 기둥 (a), (b), (c)를 제작하였다. 온도를 균일하게 △T만큼 상승시킬 때 각 기둥의 반력의 크기는? (단, A는 단면적이고, L은 길이이다)
- (a) < (b) < (c)
- (a)＝(b)＝(c)
- (a) > (b)＝(c)
- (a) > (b) > (c)
16. 그림과 같이 길이가 2 L인 단순보 AB의 중앙점에 길이가 L인 캔틸레버보 CD가 걸쳐져 있다. 점 C에 연직 하중 P가 작용할 때 하중 작용점 C의 연직 처짐은? (단, 단순보 AB와 캔틸레버보 CD의 휨강성은 모두 EI로 일정하며, 축변형과 전단변형을 무시 한다)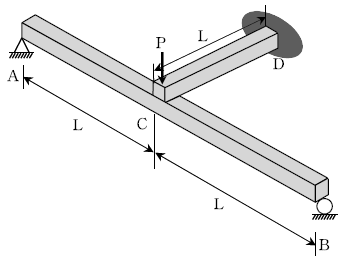
17. 그림과 같이 E, F점이 힌지인 게르버보에서 지점 C의 연직반력에 대한 영향선을 바르게 그린 것은?
- ①
- ②
- ③
- ④
18. 전체 둘레 길이가 같은 직사각형과 정사각형이 있다. 이 단면들중에서 도심축에 대한 단면계수가 최대가 되는 폭 b와 높이 h의 비는?
- 1 : 1
- 2 : 3
- 1 : 2
- 1 : 3
19. 그림과 같이 직사각형 단면을 가진 캔틸레버보의 끝단에 집중하중 P가 작용할 때, 상연으로부터 h/4 위치인 고정단의 미소면적 A에서 휨응력 σ와 전단응력 τ의 값은?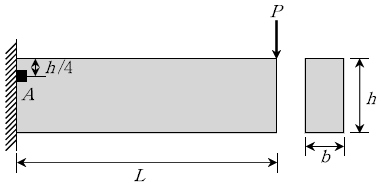
20. 그림과 같이 길이 L, 축강성 EA이며, 수평면과 기울기 를 이루고 있는 2개의 축부재 ac와 bc가 스프링상수 k인 연직스프링 cd와 절점 c에서 연결된 트러스가 있다. 절점 c에 연직 하중 P가 작용할 때, 절점 c의 연직 처짐은? (단, 스프링 상수는 k＝EA /L 이다)
-
CBT문제은행AI
2023-04-11 21:18
트러스 구조는 외력이 가해져도 내력이 발생하여 구조물이 변형되지 않는 안정적인 구조이다. 따라서, 절점 c에 가해지는 하중 P는 ac와 bc에 내력이 발생하여 변형을 막게 된다. 이 때, 연직스프링 cd는 ac와 bc 사이의 거리를 일정하게 유지하면서 변형을 흡수한다. 스프링 상수는 k＝EA /L 이므로, 연직스프링 cd의 변형량은 P/k가 된다. 따라서, 절점 c의 연직 처짐은 P/k가 된다. 이를 계산하면 "
"이 된다.