1. 다음 중 키(Key)가 전달할 수 있는 동력이 큰 순서대로 나열한 것은?
- 접선키 > 스플라인 > 세레이션 > 반달키
- 평키 > 안장키 > 묻힘키 > 스플라인
- 세레이션 > 스플라인 > 묻힘키 > 안장키
- 안장키 > 묻힘키 > 스플라인 > 세레이션
2. 압축코일 스프링에서 유효감김수(n), 코일의 평균지름(D), 와이어의 지름(d)이 모두 2배 증가된다면 같은 크기의 축방향 하중에 대해 처짐량(δ)은 어떻게 되는가?
- 1/2배 증가
- 2배 증가
- 4배 증가
- 변하지 않는다.
3. 위아래로 겹쳐진 판재의 접합을 위하여 한쪽 판재에 구멍을 뚫고, 이 구멍 안에 용가재를 녹여서 채우는 용접방법은?
- 홈 용접
- 필렛 용접
- 비드 용접
- 플러그 용접
4. 허용전단강도가 6kgf/mm2이고, 지름이 12mm인 1줄 겹치기 리벳 이음작업을 한다고 할 때, 리벳의 허용전단강도를 고려하여 6ton의 하중을 버티기 위한 리벳의 최소 수는 얼마인가?
- 6개
- 7개
- 8개
- 9개
5. 6m/s의 속도로 동력을 전달하고 있는 평벨트의 긴장측 장력이 100kgf, 이완측 장력이 50kgf일 때, 전달되는 동력(PS)은 얼마인가?
- 2PS
- 4PS
- 6PS
- 8PS
6. 기본 동정격하중 C=40kN인 단열 깊은 홈형 볼 베어링에 8×106(rev)의 회전수명을 주려고 할 때 최대 베어링 하중은 얼마인가?
- 10kN
- 20kN
- 40kN
- 80kN
7. 바깥지름 500mm, 안지름 400mm의 칼라 저널 베어링에서 1,000kgf의 하중을 받으면서 700rpm으로 회전하려면 칼라의 수는 몇 개로 하면 좋은가? (단, 발열계수의 최대허용치는 pv=0.1kgf/mm2⋅m/s으로 한다.)
- 1개
- 2개
- 3개
- 4개
8. 다음 그림과 같은 단식 블록 브레이크에서 레버에 F=120N의 힘을 가했을 때 우회전 시의 제동토크를 구하여라. (단, 마찰계수 μ=0.2, a=850mm, b=250mm, c=50mm, 드럼의 지름 D=300mm이다.)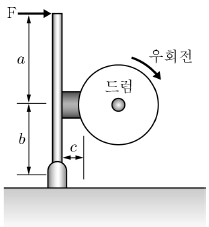
- 1.48×104[N⋅mm]
- 1.52×104[N⋅mm]
- 1.61×104[N⋅mm]
- 1.65×104[N⋅mm]
9. 두께가 20mm, 폭 100mm인 평판 중앙에 지름 40mm 구멍이 파여 있고, 평판의 양단에 9kN의 인장하중이 작용하고 있다. 구멍부분의 응력집중 계수가 Kc=2.4일 때 최대응력은 얼마인가?
- 10N/mm2
- 18N/mm2
- 20N/mm2
- 22N/mm2
10. 나사에 축 하중 Q가 작용할 때 나사부 머리부에 발생하는 전단응력 τ를 나사에서 발생하는 인장응력 σ의 0.5배까지 허용한다면 나사 머리부의 높이 H는 나사 지름 d의 몇 배가 되는가?
- 1/2
- 1
- 4/3
- 5/2
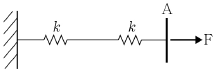
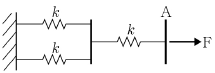
11. 다음 스프링 시스템에 같은 하중 F가 가해졌을 때, A점의 변형량이 가장 적은 것은 무엇인가? (단, k는 스프링 상수를 의미한다.)
12. 그림과 같은 단식 블록브레이크에서 우회전할 때의 레버 조작력 F1에 대한 좌회전할 때의 레버 조작력 F2의 비(F2/F1)는? (단, μ는 마찰계수이다.)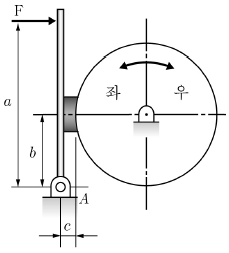
- (a+μc)/(a-μc)
- (a-μc)/(a+μc)
- (b+μc)/(b-μc)
- (b-μc)/(b+μc)
13. 비틀림각이 β인 헬리컬기어에서 잇수가 각각 30개, 120개이고 치직각 모듈이 4일 때 중심거리는?
- 150/cosβ
- 300/cosβ
- 150/cos2β
- 300/cos2β
14. 접촉면의 바깥지름이 300mm, 안지름이 100mm이고 회전수가 974rpm인 단판 마찰클러치로 1kW의 동력을 전달하는 데 필요한 축 방향으로 밀어붙이는 힘의 크기는? (단, 클러치 접촉면의 마찰계수는 0.2이다.)
- 50kgf
- 100kgf
- 150kgf
- 200kgf
15. 원동차 지름 200mm, 종동차 지름 300mm인 원통마찰차의 원동차를 10분간 600회 회전 시, 종동차는 20분간 몇 회전하는가?
- 800회전
- 1,000회전
- 1,200회전
- 1,400회전
16. 맞대기 용접이음에서 인장응력이 σt=20kgf/mm2이고, 모재의 두께는 t=5mm이며, 용접 길이가 l=20mm일 경우에 허용 하중 P는?
- 1,000kgf
- 2,000kgf
- 3,000kgf
- 4,000kgf
17. 폭경비가 1.5인 끝저널 베어링이 3,000kgf의 하중을 받고 있다. 축의 허용굽힘응력이 3kgf/mm2일 때 베어링의 길이를 구하여라.
- 87.4mm
- 105.1mm
- 118.3mm
- 131.1mm
18. 재료의 허용응력 σa=80N/mm2, 여유치수 C=1mm이고 이음매가 없는 관을 사용할 때, 안지름 D=100mm, 관 벽두께 t=8mm인 압력용기가 견딜 수 있는 최대 내부압력은 얼마인가?
- 9.2N/mm2
- 10.2N/mm2
- 11.2N/mm2
- 12.2N/mm2
19. 동적하중이 부가될 때 기어의 굽힘강도는 루이스의 공식을 이용하면 P=fvfwσbmbY와 같이 계산할 수 있다. 여기서 fv(속도계수), fw(하중계수), Y(모듈기준 치형계수)에 대한 설명으로 옳지 않은 것은?
- Y는 압력각이 클수록 크다.
- Y는 잇수가 많아질수록 크다.
- fv는 속도가 커질수록 크다.
- fw는 하중이 정적일수록 크다.
20. 원심력을 무시할 만큼의 저속의 평벨트 전동에서 유효장력이 1.5kN이고 긴장측 장력이 이완측 장력의 2배라 하면 이 벨트의 폭은 얼마로 설계해야 하는가? (단, 벨트의 허용인장응력은 5N/mm2, 벨트의 두께는 10mm, 이음효율은 80%이다.)
- 55mm
- 65mm
- 75mm
- 85mm






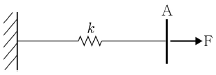

 "이다.
"이다.
- 세레이션: 키의 끝이 뾰족하게 되어 있어서, 물체를 꽉 잡아 당기는 힘이 크다.
- 스플라인: 키의 끝이 뾰족하게 되어 있어서, 물체를 꽉 잡아 당기는 힘이 크다. 또한, 키의 두께가 일정하지 않아서, 물체를 꽉 잡을 때 더욱 힘이 강하게 전달된다.
- 묻힘키: 키의 끝이 둥글게 되어 있어서, 물체를 꽉 잡아 당기는 힘이 상대적으로 약하다.
- 안장키: 키의 끝이 둥글게 되어 있어서, 물체를 꽉 잡아 당기는 힘이 상대적으로 약하다. 또한, 키의 두께가 일정하게 유지되어서, 힘이 전달되는 면적이 작아서 힘이 약하게 전달된다.