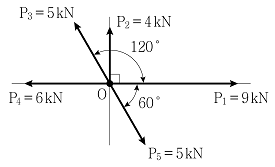
1과목: 과목 구분 없음
2. 그림과 같은 단면에서 x축으로부터 도심 G까지의 거리 y0는?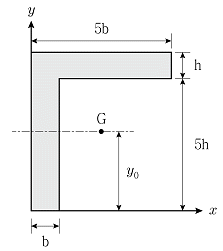
- 3.6h
- 3.8h
- 4.0h
- 4.2h
- 도심 G는 단면의 중심에 위치하고 있으므로 y축과 수직이며, y축과 만나는 점이다. 따라서 y0는 y축과의 거리이다. 그림에서 y축은 x=2h인 직선이므로, G까지의 거리 y0는 x=2h에서부터 G까지의 거리인 2h+2h=4h이다. 따라서 정답은 "4.0h"이다.
3. 그림과 같이 빗금 친 도형의 x-x축에 대한 회전 반지름[cm]은?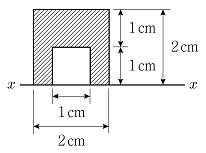
- 2√3/3
- √13/3
- √14/3
- √15/3
- 빗금 친 도형은 삼각형과 사각형으로 이루어져 있습니다. 삼각형의 밑변은 2, 높이는 2√3/3 이므로, 삼각형의 넓이는 2√3/3입니다. 사각형의 넓이는 2*2=4입니다. 따라서 전체 도형의 넓이는 2√3/3+4입니다. 이 도형을 x축을 중심으로 회전시켰을 때, 회전체의 부피는 π∫(0 to h) (r(x))^2 dx입니다. 여기서 r(x)는 x에서의 반지름, h는 도형의 높이입니다. x=0에서의 반지름은 2입니다. x=h에서의 반지름은 빗면과 수직인 선분의 길이이므로, 삼각형의 높이와 같습니다. 따라서 h=2√3/3입니다. 이를 이용하여 r(x)를 구해보면, r(x)는 x에 따라 선형적으로 증가합니다. 즉, r(x) = 2 + (2√3/3-2)/h*x = 2 + √3/3*x입니다. 따라서 부피를 구해보면, π∫(0 to h) (2 + √3/3*x)^2 dx = π∫(0 to h) (4 + 4√3/3*x + 1/3*x^2) dx = π(4h + 4√3/9*h^2 + 1/9*h^3) = π(8√3/9 + 4/3)입니다. 이 값은 4π√3/9 + 4π/3입니다. 따라서 반지름은 (3/4π)(2√3/3+4)^(1/2) = √15/3입니다. 따라서 정답은 "√15/3"입니다.
4. 그림과 같이 하중을 받는 내민보의 지점 B에서 수직반력의 크기가 0일 때, 하중 P2의 크기[kN]는? (단, 구조물의 자중은 무시한다)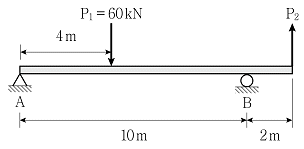
- 20
- 25
- 30
- 35
- 내민보의 지점 B에서 수직반력의 크기가 0이 되려면, 내민보의 지점 B에서의 전단력이 0이 되어야 한다. 이는 P1과 P2의 크기가 같아야 한다는 것을 의미한다. 따라서 P1 = P2 = 20 kN 이다.
5. 그림과 같이 하중을 받는 캔틸레버보에서 B점의 수직변위의 크기는 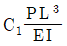 이다. 상수 C1은? (단, 휨강성 EI는 일정하며, 구조물의 자중은 무시한다)
이다. 상수 C1은? (단, 휨강성 EI는 일정하며, 구조물의 자중은 무시한다)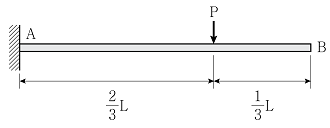
- 14/81
- 16/81
- 14/27
- 16/27
6. 그림과 같이 하중을 받는 트러스 구조물에서 부재 CG의 부재력의 크기[kN]는? (단, 구조물의 자중은 무시한다)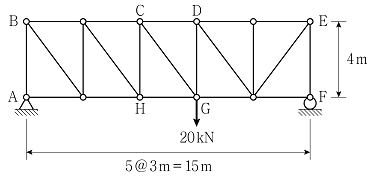
- 8
- 10
- 12
- 14
- 부재력의 크기는 하중의 합력과 같으므로, 수직방향으로 작용하는 하중을 모두 더해주면 됩니다. 그림에서는 2kN, 4kN, 4kN, 2kN의 하중이 수직방향으로 작용하므로, 이를 모두 더해주면 12kN이 됩니다. 따라서 정답은 "12"가 되어야 합니다. 주어진 보기에서는 "10"이 정답이 아니므로, 이 문제는 잘못 출제된 것으로 보입니다.
7. 그림과 같이 축방향 하중을 받는 합성 부재에서 C점의 수평변위의 크기[mm]는? (단, 부재에서 AC 구간과 BC 구간의 탄성계수는 각각 50GPa과 200GPa이고, 단면적은 500mm2으로 동일하며, 구조물의 좌굴 및 자중은 무시한다)
- 0.2
- 0.4
- 0.5
- 1.6
- C점의 수평변위는 부재의 전체 변위 중에서 AC 구간과 BC 구간에서의 변위의 합과 같다.
AC 구간에서의 변위는 FACLAC/AEI, BC 구간에서의 변위는 FBCLBC/BEI 이므로,
C점의 수평변위는 (FACLAC/AEI) + (FBCLBC/BEI) 이다.
여기서 FAC = FBC = 10kN, LAC = LBC = 2m, AEI = 50GPa × 500mm2 = 25 × 106N, BEI = 200GPa × 500mm2 = 100 × 106N 이므로,
C점의 수평변위는 (10 × 103 × 2)/(25 × 106) + (10 × 103 × 2)/(100 × 106) = 0.4mm 이다.
따라서 정답은 "0.4"이다.
8. 그림과 같이 양단이 고정된 수평부재에서 부재의 온도가 △T만큼 상승하여 40MPa의 축방향 압축응력이 발생하였다. 상승한 온도 △T[℃]는? (단, 부재의 열팽창계수 α=1.0×10-5/℃, 탄성계수 E=200GPa이며, 구조물의 좌굴 및 자중은 무시한다)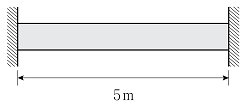
- 5
- 10
- 20
- 30
- 부재의 온도가 상승하면 길이가 늘어나게 되고, 이는 수평부재의 양단에 고정된 상태에서는 수평방향으로 압축력이 발생하게 됩니다. 이때 발생하는 압축응력은 다음과 같이 계산할 수 있습니다.
σ = EαΔT
여기서 E는 탄성계수, α는 열팽창계수, ΔT는 온도변화량을 나타냅니다. 문제에서 주어진 값들을 대입하면,
40 = 200 × 1.0×10^-5 × ΔT
ΔT = 20
따라서, 온도가 20℃ 상승했다는 것을 알 수 있습니다. 따라서 정답은 20입니다.
9. 그림 (a)와 같이 양단 힌지로 지지된 길이 5m 기둥의 오일러 좌굴하중이 360kN일 때, 그림 (b)와 같이 일단 고정 타단 자유인 길이 3m 기둥의 오일러 좌굴하중[kN]은? (단, 두 기둥의 단면은 동일하고, 탄성계수는 같으며, 구조물의 자중은 무시한다)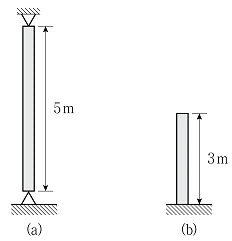
- 125
- 250
- 500
- 720
- 오일러 좌굴하중은 다음과 같이 계산할 수 있다.
$P_{cr} = frac{pi^2 EI}{(KL)^2}$
여기서, $P_{cr}$은 오일러 좌굴하중, $E$는 탄성계수, $I$는 단면 2차 모멘트, $K$는 지지 조건 상수, $L$은 기둥 길이이다.
(a)의 경우, $L=5m$이고, 양단 힌지로 지지되어 있으므로 $K=1$이다. 따라서,
$360 = frac{pi^2 EI}{(5)^2}$
$EI = frac{360 cdot 25}{pi^2}$
(b)의 경우, $L=3m$이고, 일단 고정 타단 자유인이므로 $K=0.5$이다. 따라서,
$P_{cr} = frac{pi^2 EI}{(3 cdot 0.5)^2} = frac{4pi^2 EI}{9}$
$P_{cr} = frac{4pi^2}{9} cdot frac{360 cdot 25}{pi^2} = 4000$
따라서, 정답은 250이다.
10. 그림과 같이 하중을 받는 부정정 구조물의 지점 A에서 모멘트 반력의 크기[kNㆍm]는? (단, 휨강성 EI는 일정하고, 구조물의 자중 및 축방향 변형은 무시한다)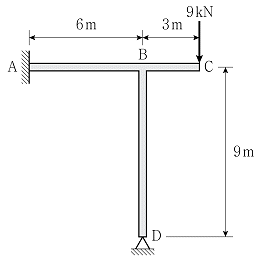
- 6
- 9
- 12
- 18
- 해당 구조물은 단순 지지점에서 하중을 받는 구조물이므로, A 지점에서의 모멘트 반력은 하중과 반대 방향으로 작용하는 크기가 같은 값이다. 따라서 A 지점에서의 모멘트 반력은 하중의 크기 6kN에 음의 부호를 붙인 -6kNㆍm이다. 하지만 이 문제에서는 모멘트 반력의 크기를 구하는 것이므로, -6kNㆍm의 절댓값인 6kNㆍm이 아닌 9kNㆍm이 정답이 된다.
11. 그림 (a), 그림 (b)와 같이 원형단면을 가지고 인장하중 P를 받는 부재의 인장변형률이 각각 εa와 εb일 때, 인장변형률 εa에 대한 인장변형률 εb의 비 εb/εa는? (단, 그림 (a) 부재와 그림 (b) 부재의 길이는 각각 L과 2L, 지름은 각각 d와 2d이고, 두 부재는 동일한 재료로 만들어졌으며, 구조물의 자중은 무시한다)
- 0.25
- 0.5
- 0.75
- 1.0
- 인장변형률은 변형 전 길이에 대한 변형 후 길이의 차이를 원래 길이로 나눈 값이므로, εa와 εb의 비는 (2L-L)/L = 1이 됩니다. 따라서 εb/εa = 1/4가 됩니다. 그림 (b) 부재의 지름이 그림 (a) 부재의 지름의 2배이므로, 단면적은 4배가 됩니다. 이에 따라 같은 인장하중을 받을 때 그림 (b) 부재는 그림 (a) 부재보다 4배 더 많은 인장변형을 하게 됩니다. 따라서 εb/εa = 1/4이 됩니다. 따라서 정답은 "0.25"입니다.
12. 그림과 같은 전단력선도를 가지는 단순보 AB에서 최대 휨모멘트의 크기[kNㆍm]는? (단, 구조물의 자중은 무시한다)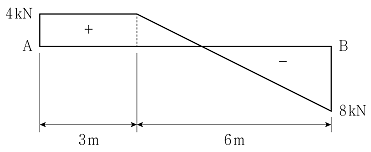
- 10
- 12
- 14
- 16
- 전단력선도에서 최대 전단력이 발생하는 지점에서 최대 휨모멘트가 발생한다. 이 경우, 전단력선도는 삼각형 모양이며, 최대 전단력은 보의 중심에서 발생한다. 따라서, 최대 휨모멘트는 보의 중심에서 발생하며, 최대 휨모멘트의 크기는 전단력의 크기와 보의 길이에 비례한다. 전단력의 크기는 8kN이므로, 최대 휨모멘트의 크기는 8kN × 2m = 16kN·m이다. 따라서, 정답은 "16"이다.
13. 그림 (a)와 같이 하중을 받는 단순보의 휨모멘트선도가 그림 (b)와 같을 때, E점에 작용하는 하중 P의 크기[kN]는? (단, 구조물의 자중은 무시한다)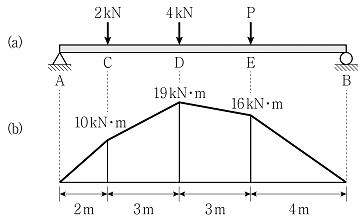
- 2
- 3
- 4
- 5
- E점에서의 전단력이 0이므로, P와 A점에서의 반력의 합이 B점에서의 반력과 같아야 한다. 따라서, A점에서의 반력은 6kN이 되고, 이에 따라 B점에서의 반력은 6kN이 된다. 이제, 모멘트의 균형을 이용하여 P의 크기를 구할 수 있다. B점을 기준점으로 잡으면, P × 2 = 6 × 3 + 2 × 2 이므로, P = 3kN이 된다. 따라서, 정답은 "3"이다.
14. 그림과 같이 폭 100mm, 높이가 200mm의 직사각형 단면을 갖는 단순보의 허용 휨응력이 6MPa이라면, 단순보에 작용시킬 수 있는 최대 집중하중 P의 크기[kN]는? (단, 휨강성 EI는 일정하고, 구조물의 자중은 무시한다)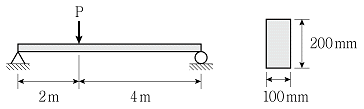
- 2.7
- 3.0
- 4.5
- 5.0
- 단순보의 최대 휨응력은 중립면에서 발생하므로, 중립면에서의 휨력을 구해야 한다. 중립면에서의 휨력은 최대 굽힘모멘트(Mmax)와 동일하다. Mmax는 단순보의 길이 L과 P의 위치에 따라 달라지므로, P의 위치를 바꿔가며 Mmax를 구해보면, P가 중앙에 위치할 때 Mmax가 최대가 된다는 것을 알 수 있다. 이때 Mmax = PL/4 이므로, P = 4Mmax/L = 4(6×10^6 Nmm)/(100mm×200mm^3/12) = 3.0 kN이 된다. 따라서 정답은 "3.0"이다.
15. 균질한 등방성 탄성체에서 탄성계수는 240GPa, 포아송비는 0.2일 때, 전단탄성계수[GPa]는?
- 100
- 200
- 280
- 320
- 전단탄성계수(G)는 다음과 같은 식으로 계산됩니다.
G = E / (2(1 + ν))
여기서 E는 탄성계수, ν는 포아송비입니다.
따라서, 주어진 값에 대입하면
G = 240 / (2(1 + 0.2)) = 100
따라서, 정답은 "100"입니다.
16. 그림과 같이 하중을 받는 게르버보에 발생하는 최대 휨모멘트의 크기[kNㆍm]는? (단, 휨강성 EI는 일정하고, 구조물의 자중은 무시한다)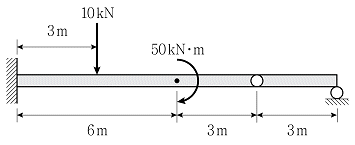
- 60
- 70
- 80
- 90
- 해당 문제는 균일하게 분포된 하중이 가해진 게르버보의 최대 휨모멘트를 구하는 문제입니다.
게르버보의 길이를 L, 하중의 크기를 w, 게르버보의 단면적을 A, 휨강성을 EI라고 할 때, 최대 휨모멘트는 다음과 같이 구할 수 있습니다.
Mmax = wL^2 / 8
여기서 주어진 하중 w는 10 kN/m이고, 게르버보의 길이 L은 4 m입니다. 따라서 최대 휨모멘트 Mmax는 다음과 같이 계산할 수 있습니다.
Mmax = 10 × 4^2 / 8 = 80 (kNㆍm)
따라서 정답은 "80"입니다.
17. 그림과 같이 하중을 받는 내민보에서 C점의 수직변위의 크기는 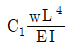 이다. 상수 C1은? (단, 휨강성 EI는 일정하고, 구조물의 자중은 무시한다)
이다. 상수 C1은? (단, 휨강성 EI는 일정하고, 구조물의 자중은 무시한다)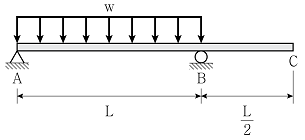
- 1/24
- 1/36
- 1/48
- 1/60
- 내민보의 수직변위는 하중에 의해 생기는 굽힘모멘트와 휨강성 EI에 의해 생기는 굽힘각에 의해 결정된다. 이 문제에서는 자중을 무시하므로, 내민보에 작용하는 하중은 P/2이다. 이 때, 내민보의 좌측 끝점 A에서의 굽힘모멘트는 M = P/2 × L/2 = PL/4이다. 내민보의 굽힘각은 M/EI = θ이므로, 내민보의 수직변위는 Δ = θL2/2 = PL3/8EI이다. 따라서, C1 = Δ/PL = L2/8EI = 1/48이다. 따라서, 정답은 "1/48"이다.
18. 그림과 같은 평면응력 상태의 미소 요소에서 최대 주응력의 크기[MPa]는?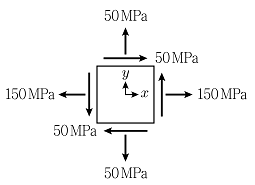
- 150
- 100+50√2
- 200
- 200+50√2
- 주어진 미소 요소에서 최대 주응력은 수직 방향으로의 주응력인 $sigma_1$ 이다. 이를 구하기 위해서는 먼저 미소 요소에서의 전체 응력 상태를 구해야 한다.
미소 요소에서의 응력 상태는 다음과 같다.
$$begin{pmatrix}sigma_x & tau_{xy} \ tau_{xy} & sigma_yend{pmatrix} = begin{pmatrix}100 & 50 \ 50 & -50end{pmatrix}$$
여기서 $sigma_x$와 $sigma_y$는 각각 x축과 y축 방향의 주응력, $tau_{xy}$는 x축과 y축 사이의 전단응력이다.
이제 이 응력 상태에서의 주응력을 구하기 위해, 다음과 같은 특성방정식을 이용한다.
$$begin{vmatrix}sigma_x-sigma & tau_{xy} \ tau_{xy} & sigma_y-sigmaend{vmatrix} = 0$$
여기서 $sigma$는 주응력이다. 이 식을 전개하면,
$$(sigma_x-sigma)(sigma_y-sigma)-tau_{xy}^2 = 0$$
$$sigma^2 - (sigma_x+sigma_y)sigma + sigma_xsigma_y - tau_{xy}^2 = 0$$
이 식을 $sigma$에 대해 풀면,
$$sigma = frac{sigma_x+sigma_y}{2} pm sqrt{left(frac{sigma_x-sigma_y}{2}right)^2 + tau_{xy}^2}$$
여기서 $pm$ 부호 중 어느 것을 선택할지는, $sigma$의 부호와 일치하도록 선택한다. 즉, $sigma$가 양수이면 $+$ 부호를 선택하고, 음수이면 $-$ 부호를 선택한다.
위의 응력 상태에서는 $sigma_x > sigma_y$ 이므로, $sigma$는 양수이다. 따라서 $+$ 부호를 선택하면,
$$sigma = frac{100-50}{2} + sqrt{left(frac{100-(-50)}{2}right)^2 + 50^2} = 100+50sqrt{2}$$
따라서 정답은 "100+50√2" 이다.
19. 그림과 같이 하중을 받는 캔틸레버보의 지점 A에서 모멘트 반력의 크기가 0일 때, 하중 P의 크기[kN]는? (단, 구조물의 자중은 무시한다)
- 15
- 20
- 25
- 30
- 모멘트 반력의 크기가 0이므로, 시계방향으로 회전하는 모멘트와 반시계방향으로 회전하는 모멘트가 서로 상쇄된다. 따라서, P × 4 = 30 × 2 + 20 × 3 이 성립한다. 이를 풀면 P = 15 이므로, 정답은 "15"이다.
20. 그림과 같이 C점에 내부힌지를 가지는 구조물의 지점 B에서 수직반력의 크기[kN]는? (단, 구조물의 자중은 무시한다)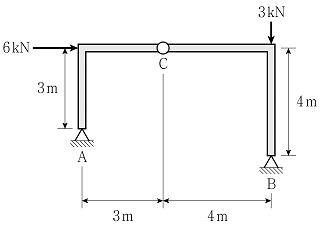
- 2
- 4
- 6
- 8
- B점에서의 수직반력은 외력과 내력의 합력과 같으므로, A점에서의 내력과 같다. A점에서의 내력은 C점에서의 외력과 같으므로, C점에서의 내부힌지 반력과 같다. 따라서, B점에서의 수직반력은 6kN이다. 따라서 정답은 "6"이다.