1과목: 과목 구분 없음
1. b=300㎜, d=600㎜인 단철근 직사각형보의 등가직사각형 응력블록의 깊이 a = 100㎜일 때, 철근량 As[mm2]는? (단, fck=20MPa, fy=300MPa이며, 2012년도 콘크리트구조기준을 적용한다)
- 850
- 1,550
- 1,700
- 3,400
2. 단순 지지된 보에 등분포 고정하중이 작용하고 있다. 순간 탄성 처짐이 20㎜일 경우 5년 뒤의 총 처짐량[㎜]은? (단, 중앙 단면의 압축 철근비는 0.02이며, 2012년도 콘크리트구조기준을 적용한다)
- 20
- 25
- 30
- 40
3. 그림과 같은 철근콘크리트 단면에서 균열 모멘트 Mcr[kNㆍm]은? (단, 콘크리트는 보통 골재를 사용하고, fck=25MPa이며, 2012년도 콘크리트구조기준을 적용한다)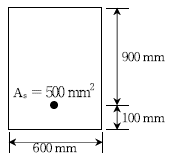
- 315
- 420
- 3,150
- 4,200
4. 물-시멘트비(W/C) 50%, 단위수량 140kgf/m3, 단위잔골재량 760 kgf/m3인 배합을 실시하여 콘크리트의 단위중량을 측정한 결과 2,300kgf/m3일 때, 콘크리트의 단위굵은골재량[kgf/m3]은? (단, 시멘트의 비중은 3.15, 잔골재의 비중은 2.60, 굵은 골재의 비중은 2.65이고, 혼화재료는 사용하지 않았다)
- 1,120
- 1,220
- 1,260
- 1,400
5. 직사각형 철근콘크리트 단면이 전단철근 없이 계수전단력 Vu =75 kN을 저항할 수 있는 단면의 최소 유효깊이 d [㎜]는? (단, fck=16MPa, 단면의 폭 b=400㎜이며, 2012년도 콘크리트 구조기준을 적용한다)
- 600
- 750
- 850
- 1,000
6. 그림과 같은 확대기초에 계수 하중 Pu =1,200 kN이 작용할 때, 전단에 대한 위험단면의 둘레 길이 b0 [㎜]는? (단, 2012년도 콘크리트구조기준을 적용한다)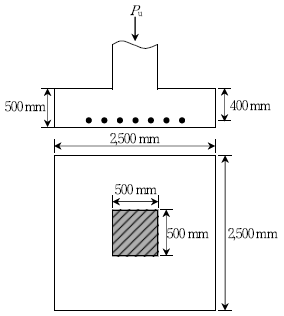
- 3,600
- 4,000
- 4,400
- 4,500
7. 그림과 같이 옹벽의 무게 W=90 kN이고 옹벽에 작용하는 수평력 H=20 kN일 때, 전도에 대한 안전율과 활동에 대한 안전율은? (단, 옹벽의 무게 및 수평력은 단위폭당 값이며 옹벽의 저판 콘크리트와 흙 사이의 마찰계수는 0.4이고, 2012년도 콘크리트 구조기준을 적용한다) (순서대로 전도에 대한 안전율, 활동에 대한 안전율)
- 3.0, 1.5
- 3.0, 1.8
- 6.0, 1.5
- 6.0, 1.8
8. 그림과 같이 지간 L=10m인 프리스트레스트 콘크리트 단순보에 자중을 포함한 등분포하중 w=40kN/m가 작용하고 있다. 긴장재는 지간 중앙에 편심 e=0.4m로 절곡 배치하였다. 긴장력 P=1,000 kN일 때, 보의 끝단에서 전단력이 작용하지 않는 지점까지의 거리x[m]는? (단, sinθ=2e/L로 가정하고, 프리스트레스의 손실은 무시한다)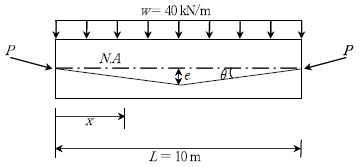
- 1
- 2
- 3
- 4
9. 그림과 같이 리벳의 직경이 20mm일 때, 이 리벳의 강도[kN]는? (단, 리벳의 허용 전단응력va=130MPa, 허용 지압응력fba=300MPa 이다)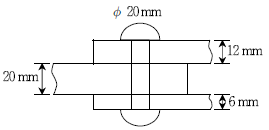
- 26π
- 52π
- 108
- 216
10. 길이가 2 m이고 사각형 단면(200mm× 200mm)인 기둥에 연직 하중 80 kN이 고정하중으로 작용한다. 기둥이 옥외에 있을 때, 크리프 변형률(ϵc)은? (단, 콘크리트의 탄성계수 Ec=20,000MPa이며, 2012년도 콘크리트구조기준을 적용한다)
- 0.0001
- 0.0002
- 0.0003
- 0.003
11. 옹벽의 안정조건에 대한 설명으로 옳지 않은 것은? (단, 2012년도 콘크리트구조기준을 적용한다)
- 활동에 대한 저항력은 옹벽에 작용하는 수평력의 1.5배 이상이어야 한다.
- 지반에 유발되는 최대 지반반력은 지반의 허용지지력을 초과할 수 없다.
- 전도에 대한 저항휨모멘트는 횡토압에 의한 전도모멘트의 2배이상이어야 한다.
- 지반의 허용지지력은 지반의 극한지지력의 3배 이상이어야 한다.
12. 지름이 150 mm, 높이 300 mm인 원주형 표준공시체에 대하여 쪼갬인장시험을 실시한 결과, 파괴 시 하중이 270,000 N이었다면 콘크리트의 쪼갬인장강도[MPa]는? (단, π=3으로 계산한다)
- 1.5
- 2.0
- 3.5
- 4.0
13. 그림과 같은 철근 콘크리트 독립확대기초의 지반에 발생하는 최대 및 최소 지반 응력(qmax, qmin[kN/m2])은? (단, 기초의 자중은 무시하고, 응력은 단위폭당 계산한다) (순서대로 qmax, qmin)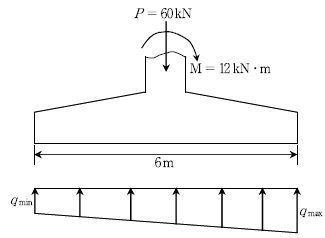
- 10, 6
- 10, 8
- 12, 6
- 12, 8
14. 그림과 같이 단순 지지된 슬래브의 중앙점에 집중하중 P=76kN이 작용할 때, ab방향에 분배되는 하중[kN]은?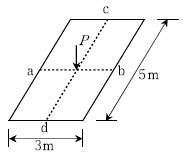
- 50
- 60.5
- 62.5
- 125
15. 그림과 같은 단철근 T형보에서 플랜지 부분에 대응하는 철근량 Asf[mm2]는? (단, fck=30MPa, fy=300MPa이며, 2012년도 콘크리트구조기준을 적용한다)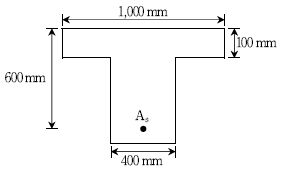
- 3,400
- 4,000
- 5,100
- 5,200
16. 그림과 같이 b=300mm, d=500mm인 철근콘크리트 캔틸레버보에 자중을 포함한 계수등분포하중 wu=50 kN/m가 작용하고 있다. 전단에 대한 위험단면에서 전단철근이 부담해야 할 공칭전단강도 Vs의 최소값[kN]은? (단, 콘크리트는 보통골재를 사용하고, fck=25MPa, fy=300MPa이며, 2012년도 콘크리트구조기준을 적용한다)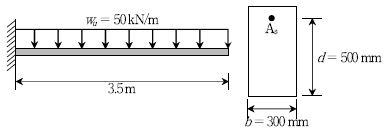
- 52
- 66.7
- 75
- 120.5
17. 단면의 폭b=300mm, 유효깊이d=500mm인 단철근 직사각형보가 등가 직사각형의 응력깊이 a=170mm, fck=28MPa, fy=400MPa인 경우 강도감소계수는? (단, 압축지배단면에서 강도감소계수는 0.65로 계산하며, 소수 넷째자리에서 반올림하고, 2012년도 콘크리트 구조기준을 적용한다)
- 0.817
- 0.833
- 0.842
- 0.850
18. 그림과 같이 프리스트레스트 콘크리트 단순보 단면의 중심에 PS강선이 배치된 부재에 자중을 포함한 등분포하중 w=4 kN/m가 작용한다. 이 부재에 인장응력이 발생하지 않으려면 PS강선에 도입되어야 할 최소 긴장력 P [kN]는?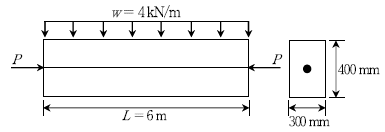
- 150
- 270
- 390
- 430
19. 압축연단에서 중립축까지의 거리 c=120mm인 단철근 직사각형보의 단면이 인장지배 단면이 되기 위한 인장철근의 최소 유효깊이 d [mm]는? (단, 인장철근은 1단 배근되어 있고, 철근의 탄성계수 Es=200,000MPa, fy=500MPa이며, 2012년도 콘크리트구조기준을 적용한다)
- 200
- 280
- 320
- 370
20. 그림과 같이 두께가 10 mm인 강판을 리벳으로 연결한 경우 강판이 최대로 허용할 수 있는 인장력 P [kN]는? (단, 강판의 허용 인장응력 fta=150MPa, 리벳구멍의 지름 25mm이다)
- 135
- 155
- 175
- 195






a = 0.5d - 0.5√(d^2 - 4b^2)
여기서 b는 보의 너비, d는 보의 높이입니다. 따라서 b=300mm, d=600mm로 대입하면,
a = 0.5(600) - 0.5√(600^2 - 4(300^2)) ≈ 100mm
따라서 응력블록의 깊이는 100mm입니다.
철근의 단면적은 다음과 같이 구할 수 있습니다.
As = (0.85fctk/fy)bd
여기서 fctk는 콘크리트의 특성강도, fy는 철근의 항복강도, b는 보의 너비, d는 보의 높이입니다. 따라서 fctk=20MPa, fy=300MPa, b=300mm, d=600mm로 대입하면,
As = (0.85×20/300)×300×600 ≈ 1,700mm^2
따라서 철근량 As는 1,700mm^2입니다.